cg

多边形裁减 - Sutherland Hodgman算法

前言

之前在做矢量地图相关内容时用到了boost库，但是在进行矢量切片时，我发现boost::geometry::intersection存在bug：boost::intersection produces wrong results。回想起计算机图形学一书中有提到相关内容，回去翻看，于是发现了Sutherland Hodgman算法。
mapbox的开源切片工具也使用了Sutherland Hodgman算法。

Sutherland Hadgman 算法

Sutherland Hodgman 算法是一种使用凸多边形裁减凸多边形的算法。如同其他裁减算法一样， Sutherland Hodgman算法也是每次使用裁减窗口的一条边去裁减目标，当所有的边都裁剪以后，得到的就是最终的结果了。

算法主要内容如下：
用一条边e裁减目标多边形时，对于多边形的每一条边PQ，可能会有如下4种场景：

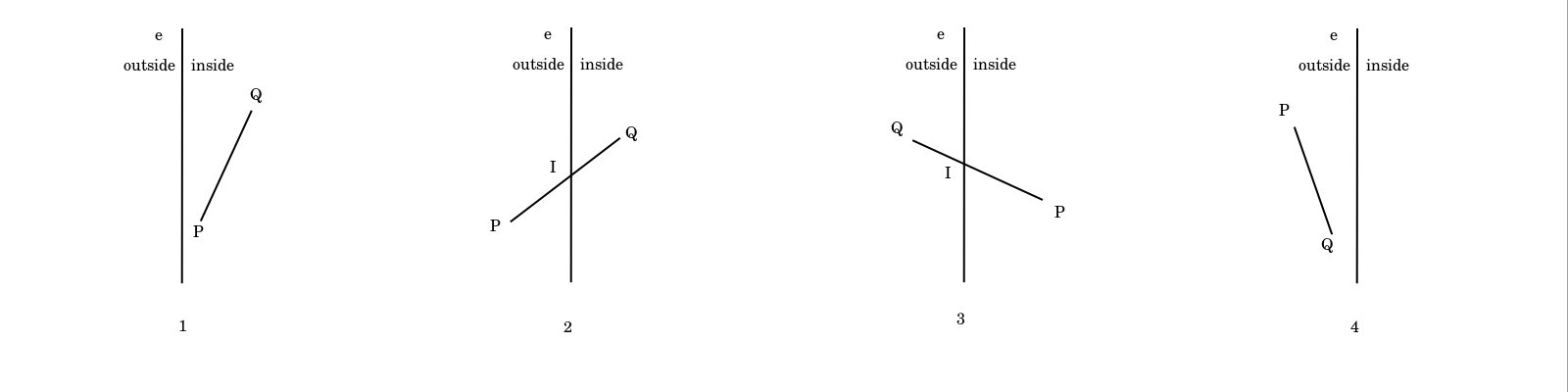
图中inside代表裁减窗口内部。对于这4种场景，采取动作如下：

  1. 保留Q点
  2. 保留交点I和Q点
  3. 保留交点I
  4. 不保留任何点

例如，用边e裁减矩形ABCD:

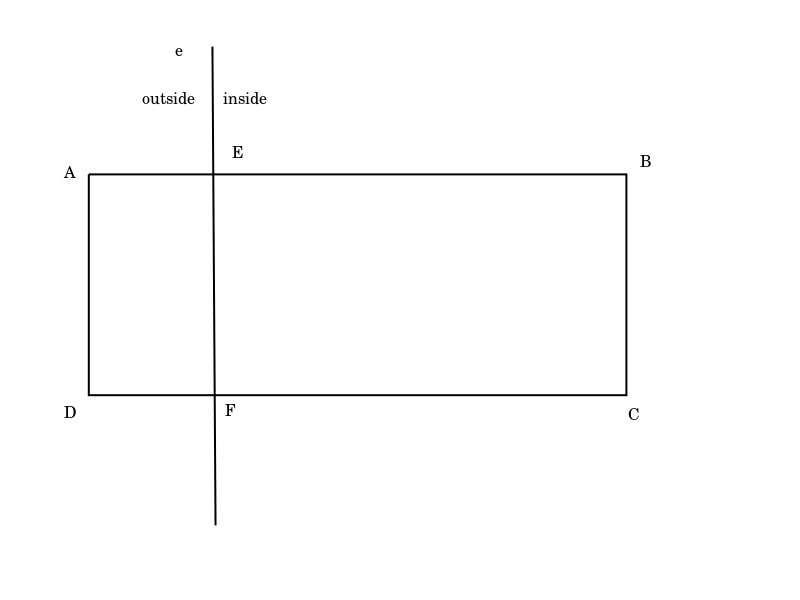
有如下流程：

  1. 边AB满足场景2，保留交点E和终点B
  2. 边BC满足场景1，保留终点C
  3. 边CD满足场景3，保留交点F
  4. 边DA满足场景4，不保留任何点

最终得到矩形EBCF。

注意：点在边上作为点在内部处理。

相关定义及算法伪码

假设有基础数据类型定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
struct point
{
	float x, y;
};
struct line
{
	point a, b;
};
struct polygon
{
	vector<point> points;
	vector<point> normals; // normal of each edge
};

则， Sutherland Hodgman 伪码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
polygon sutherland_hodgman(polygon poly, polygon wnd)
{
	vector<point> pts(poly.points());
	vector<point> tmp;
	for(line l : wnd.edges)
	{
		line nm = wnd.normals(l);
		for(point cur : pts)
		{
			point n = next_point(pts, cur);
			line e(cur, n);
			
			int state = 0;
			if(outside(n, nm)) state |= 0x1;
			if(outside(cur, nm)) state |= 0x2;
			
			swith(state)
			{
			case 0: // both inside
				tmp.push(n);
			case 1: // leave poly.
				tmp.push(intersection(l, e)); break;
			case 2: // enter poly
			{
				tmp.push(intersection(l, e));
				tmp.push(n);
			}break;
			case 3: // both outside, do nothing.
			}
		}
		pts.swap(tmp);
	}
	return polygon(pts);
}

矩形裁剪框下的Sutherland Hodgman

对于任意的多边形裁剪窗来说，要判断点的位置比较麻烦，需要计算裁减窗口每条边的法向量，然后通过点积进行比较。
同样，求两条边的交点也很麻烦。

但是，一般情况下，裁减窗口都是一个矩形，而且是一个水平放置的矩形。那么这个过程就非常轻松愉快了。

假设矩形裁减窗口定义如下：

1
2
3
4
struct rect
{
    double l, t, r, b; // left top right bottom
};

例如，当使用矩形的 l 进行裁减时，要判断点的位置，直接 pt.y < rect.l 即可。
而求交点，就是求 x = l 时的 y 值。

使用矩形窗口进行裁减的整个流程可以用如下伪码表示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
polygon sutherland_hodgman(polygon poly, rect rc)
{
    vector<point> pts(poly.points);
	vector<point> tmp;
    
    point P = first_point(poly);
    // clip with top edge
    for(point cur : pts)
    {
		point n = next_point(pts, cur);
        int state = 0;
        if(n.y < rc.l) state |= 0x1;
        if(cur.y < rc.l) state |= 0x2;
        
        switch(state)
        {
			// add points to tmp ...
		}
    }
    pts.swap(tmp);
    
    // clip with bottom
    ...
    // clip with left edge
    ...
    // clip with right edge
    ...
    return polygon(pts);
}

单看代码的话，可能会感觉反而变复杂了，但实际编码难度则小了不少，性能也有所提高。

跑一个简单的 benchmark, 得到数据如下：

vol sh sh_rc
1w 104 10
10w 1031 89
100w 10365 887

表中， sh 代表普通 sutherland hodgman 算法实现，矩形裁减窗口也是使用 polygon 定义。sh_gl 代表使用 rect 类型作为裁减窗口的算法实现。

可以看出，矩形裁减窗口下，算法效率提高了10倍以上。

以上的实现代码可以在这里找到。

存在的问题

如书上描述的那样，Sutherland Hodgman是用凸多边形裁剪凸多边形的算法，如果用来处理凹多边形，则会有一些问题。

考虑如下的场景：

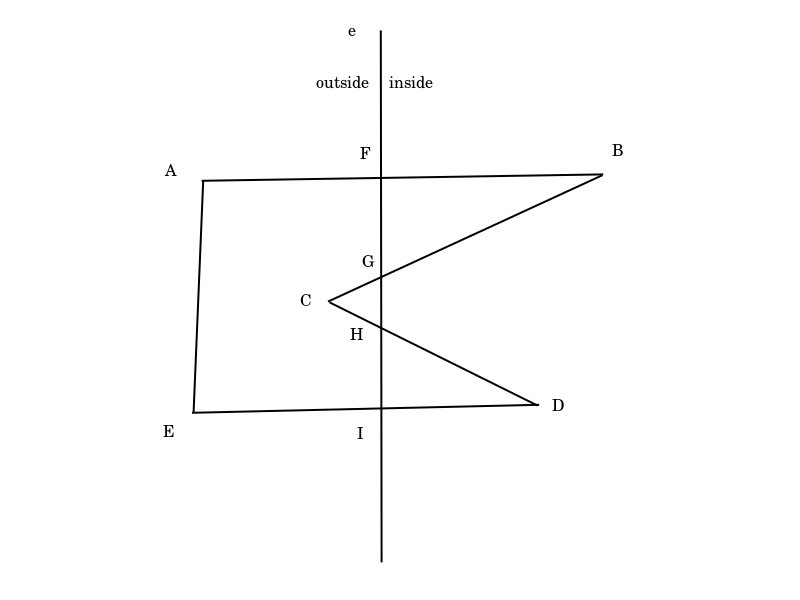
用边e裁剪凹多边形ABCDE，按照直观来看，应该得到两个小三角形FBG和HDI。但是按照Sutherland Hodgman算法的流程，只会得到一个点序列FBGHDI，其中，边IF和GH实际上重叠了。

如wiki所述，这对渲染不会造成影响。Mapbox的开源工具正是这样进行矢量数据裁剪。并且，为了解决矢量瓦片边框问题，裁剪窗口总是比显示窗口要大的，所以上面这个例子中两个小三角形的连接处是永远不会被渲染，最终的效果应该是这样：

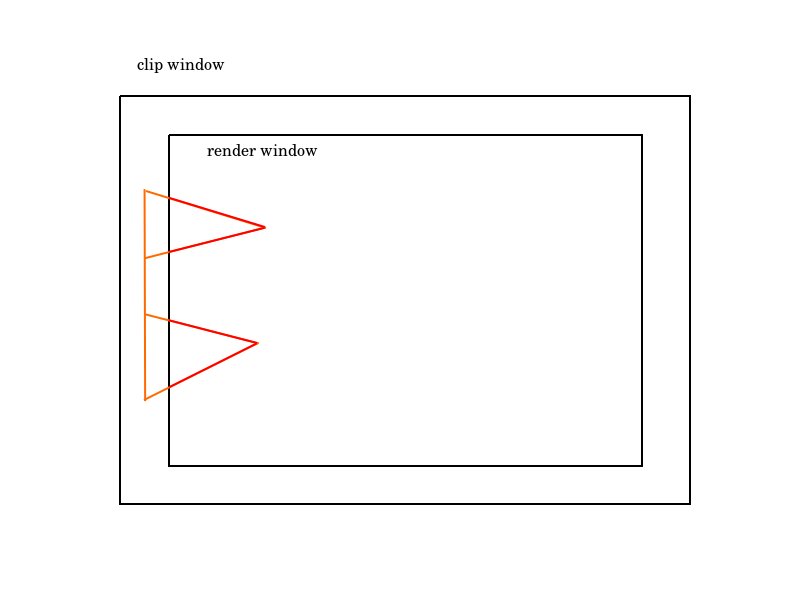
至于怎么裁减这样的凹多边形，就留到后面的文章吧 :D